Erlang 入门

为美好的未来！

• 首页
• 常见问题
• RSS
• 代码

用函数式方法解决问题

逆波兰表达式计算器

大多数人学习用运算符位于数字之间的方式编写算术表达式 ((2 + 2) / 5)。这正是大多数计算器让您插入数学表达式的方式，也是您在学校学习算数时被教导的记法。这种记法有一个缺点，那就是你需要了解运算符优先级：乘法和除法比加法和减法更重要（具有更高的 *优先级*）。

还存在另一种记法，称为 *前缀记法* 或 *波兰记法*，其中运算符位于操作数之前。在这种记法下，(2 + 2) / 5 将变成 (/ (+ 2 2) 5)。如果我们决定说 + 和 / 始终接受两个参数，那么 (/ (+ 2 2) 5) 可以简单地写成 / + 2 2 5。

但是，我们将重点关注 *逆波兰记法*（或简称为 *RPN*），它是前缀记法的反面：运算符位于操作数之后。上述相同示例在 RPN 中将写成 2 2 + 5 /。其他示例表达式可以是 9 * 5 + 7 或 10 * 2 * (3 + 4) / 2，它们分别转换为 9 5 * 7 + 和 10 2 * 3 4 + * 2 /。这种记法在早期的计算器模型中被广泛使用，因为它只需要很少的内存即可使用。事实上，有些人仍然随身携带 RPN 计算器。我们将编写一个这样的计算器。

首先，了解如何阅读 RPN 表达式可能很有帮助。一种方法是逐个找到运算符，然后根据它们的参数个数将它们与其操作数分组。

10 4 3 + 2 * -
10 (4 3 +) 2 * -
10 ((4 3 +) 2 *) -
(10 ((4 3 +) 2 *) -)
(10 (7 2 *) -)
(10 14 -)
-4

但是，在计算机或计算器的上下文中，更简单的方法是当我们看到操作数时，将它们全部放入一个 *堆栈* 中。以数学表达式 10 4 3 + 2 * - 为例，我们看到的第一个操作数是 10。我们将它添加到堆栈中。然后是 4，所以我们也将其压入堆栈顶部。第三个是 3；我们也将其压入堆栈中。现在我们的堆栈应该看起来像这样

要解析的下一个字符是 +。它是一个参数个数为 2 的函数。为了使用它，我们需要为它提供两个操作数，这些操作数将从堆栈中获取。

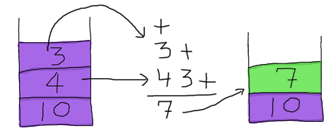
因此，我们获取该 7 并将其压回堆栈顶部（哎呀，我们不想让这些肮脏的数字到处飘浮！）。现在堆栈为 [7,10]，表达式中剩下的部分是 2 * -。我们可以取 2 并将其压入堆栈顶部。然后我们看到 *，它需要两个操作数才能工作。同样，我们从堆栈中获取它们。

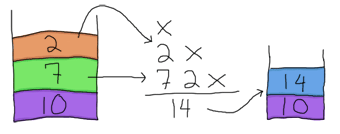
并将 14 压回堆栈顶部。剩下的只是 -，它也需要两个操作数。太棒了！我们的堆栈中还剩两个操作数。使用它们！

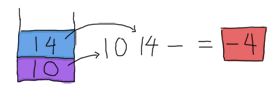
因此我们得到了结果。这种基于堆栈的方法相对来说很可靠，而且在开始计算结果之前需要进行的解析工作量很少，这解释了为什么旧式计算器使用这种方法是一个好主意。还有其他使用 RPN 的原因，但这超出了本指南的范围，因此您可能需要查看 维基百科文章。

一旦我们完成了复杂的部分，在 Erlang 中编写这个解决方案并不难。事实证明，困难的部分是弄清楚为了获得最终结果需要执行哪些步骤，而我们刚刚做到了。很好。打开一个名为 calc.erl 的文件。

首先要考虑的是我们如何表示一个数学表达式。为了简单起见，我们可能会将它们输入为一个字符串："10 4 3 + 2 * -"。这个字符串包含空格，这些空格不是我们解决问题过程的一部分，但对于使用简单的词法分析器来说是必要的。那么，经过词法分析器处理后，["10","4","3","+","2","*","-"] 形式的项列表将是可以使用的。事实证明，string:tokens/2 函数正是这样做的。

1> string:tokens("10 4 3 + 2 * -", " ").
["10","4","3","+","2","*","-"]

这将是我们表达式的良好表示形式。下一个要定义的部分是堆栈。我们该如何做到这一点？您可能已经注意到，Erlang 的列表的行为很像堆栈。在 [Head|Tail] 中使用 cons (|) 运算符实际上与将 Head 压入堆栈顶部（在本例中为 Tail）的行为相同。使用列表作为堆栈就足够了。

要读取表达式，我们只需按照手工解决问题时所做的那样即可。从表达式中读取每个值，如果它是数字，则将其放入堆栈中。如果它是函数，则从堆栈中弹出它所需的所有值，然后将结果压回堆栈中。为了泛化，我们只需要遍历整个表达式一次，并将结果累积起来。听起来像是 fold 的完美工作！

我们需要计划的是 lists:foldl/3 将应用于表达式中每个运算符和操作数的函数。这个函数，因为它将在 fold 中运行，将需要接受两个参数：第一个参数将是表达式中要处理的元素，第二个参数将是堆栈。

我们可以在 calc.erl 文件中开始编写代码。我们将编写负责所有循环的函数，以及从表达式中删除空格的函数。

-module(calc).
-export([rpn/1]).

rpn(L) when is_list(L) ->
    [Res] = lists:foldl(fun rpn/2, [], string:tokens(L, " ")),
    Res.

接下来我们将实现 rpn/2。请注意，由于表达式的每个运算符和操作数最终都将被压入堆栈顶部，因此已解决的表达式的结果将位于该堆栈上。我们需要在将结果返回给用户之前，将最后一个值从堆栈中取出。这就是为什么我们对 [Res] 进行模式匹配，并且只返回 Res 的原因。

好了，现在进入更难的部分。我们的 rpn/2 函数将需要为传递给它的所有值处理堆栈。函数的头部可能看起来像 rpn(Op,Stack)，它的返回值像 [NewVal|Stack]。当我们遇到普通数字时，操作将是

rpn(X, Stack) -> [read(X)|Stack].

在这里，read/1 是一个将字符串转换为整数或浮点数的函数。遗憾的是，Erlang 中没有内置函数可以做到这一点（只能实现其中之一）。我们将自己添加它。

read(N) ->
    case string:to_float(N) of
        {error,no_float} -> list_to_integer(N);
        {F,_} -> F
    end.

其中 string:to_float/1 将字符串（如 "13.37"）转换为等效的数值。但是，如果没有办法读取浮点数，它将返回 {error,no_float}。发生这种情况时，我们需要改为调用 list_to_integer/1。

现在回到 rpn/2。我们遇到的数字都会被添加到堆栈中。但是，由于我们的模式匹配任何内容（参见 模式匹配），运算符也将被压入堆栈中。为了避免这种情况，我们将把它们全部放在前面的子句中。我们将尝试第一个使用这种方法的是加法。

rpn("+", [N1,N2|S]) -> [N2+N1|S];
rpn(X, Stack) -> [read(X)|Stack].

我们可以看到，每当我们遇到 "+" 字符串时，我们都会从堆栈顶部获取两个数字 (N1,N2)，并将它们相加，然后将结果压回该堆栈中。这正是我们手工解决问题时应用的相同逻辑。尝试程序，我们可以看到它可以正常工作。

1> c(calc).
{ok,calc}
2> calc:rpn("3 5 +").
8
3> calc:rpn("7 3 + 5 +").
15

剩下的部分很简单，您只需添加所有其他运算符即可。

rpn("+", [N1,N2|S]) -> [N2+N1|S];
rpn("-", [N1,N2|S]) -> [N2-N1|S];
rpn("*", [N1,N2|S]) -> [N2*N1|S];
rpn("/", [N1,N2|S]) -> [N2/N1|S];
rpn("^", [N1,N2|S]) -> [math:pow(N2,N1)|S];
rpn("ln", [N|S])    -> [math:log(N)|S];
rpn("log10", [N|S]) -> [math:log10(N)|S];
rpn(X, Stack) -> [read(X)|Stack].

请注意，只接受一个参数的函数（例如对数）只需要从堆栈中弹出 一个元素。将添加诸如 'sum' 或 'prod' 之类的函数作为练习留给读者，这些函数返回迄今为止读取的所有元素的总和或所有元素的乘积。为了帮助您，这些函数在我的 calc.erl 版本中已经实现了。

为了确保所有这些都能正常工作，我们将编写非常简单的单元测试。Erlang 的 = 运算符可以充当 *断言* 函数。断言在遇到意外值时应该崩溃，这正是我们需要的。当然，Erlang 还有更高级的测试框架，包括 Common Test 和 EUnit。我们稍后会查看它们，但就目前而言，基本的 = 就可以完成这项工作。

rpn_test() ->
    5 = rpn("2 3 +"),
    87 = rpn("90 3 -"),
    -4 = rpn("10 4 3 + 2 * -"),
    -2.0 = rpn("10 4 3 + 2 * - 2 /"),
    ok = try
        rpn("90 34 12 33 55 66 + * - +")
    catch
        error:{badmatch,[_|_]} -> ok
    end,
    4037 = rpn("90 34 12 33 55 66 + * - + -"),
    8.0 =  rpn("2 3 ^"),
    true = math:sqrt(2) == rpn("2 0.5 ^"),
    true = math:log(2.7) == rpn("2.7 ln"),
    true = math:log10(2.7) == rpn("2.7 log10"),
    50 = rpn("10 10 10 20 sum"),
    10.0 = rpn("10 10 10 20 sum 5 /"),
    1000.0 = rpn("10 10 20 0.5 prod"),
    ok.

测试函数尝试所有操作；如果没有引发异常，则测试被认为成功。前四个测试检查基本算术函数是否按预期工作。第五个测试指定了尚未解释的行为。try ... catch 预计会抛出一个 badmatch 错误，因为表达式无法工作。

90 34 12 33 55 66 + * - +
90 (34 (12 (33 (55 66 +) *) -) +)

在 rpn/1 的末尾，值 -3947 和 90 留在堆栈中，因为没有运算符可以对挂在那里 的 90 进行操作。可以采用两种方法来解决这个问题：要么忽略它，只取堆栈顶部的值（这将是最后计算的结果），要么因为算术错误而崩溃。考虑到 Erlang 的策略是让它崩溃，因此在这里选择了这种策略。实际导致崩溃的部分是 rpn/1 中的 [Res]。这确保了堆栈中只留下一个元素，即结果。

形式为 true = FunctionCall1 == FunctionCall2 的几个测试是存在的，因为您不能在 = 的左侧使用函数调用。它仍然像断言一样工作，因为我们将比较的结果与 true 进行比较。

我还添加了 sum 和 prod 运算符的测试用例，以便您可以练习自己实现它们。如果所有测试都成功，您应该看到以下内容

1> c(calc).
{ok,calc}
2> calc:rpn_test().
ok
3> calc:rpn("1 2 ^ 2 2 ^ 3 2 ^ 4 2 ^ sum 2 -").
28.0

其中 28 确实等于 sum(1² + 2² + 3² + 4²) - 2。您可以随意尝试其中的任何一个。

为了使我们的计算器更完善，可以做的一件事是，确保它在由于未知运算符或堆栈中剩余的值而崩溃时引发 badarith 错误，而不是我们当前的 badmatch 错误。这当然会使 calc 模块的用户更容易调试。

希思罗机场到伦敦

我们的下一个问题也来自 Haskell 入门。您乘坐的飞机将在未来几个小时内降落在希思罗机场。您必须尽快赶到伦敦；您的富有的叔叔病危，您想成为第一个到达那里的人，以便宣称对他的财产拥有所有权。

从希思罗机场到伦敦有两条路，以及许多连接它们的较小街道。由于限速和通常的交通状况，某些路段和较小街道的驾驶时间比其他路段更长。在你降落之前，你决定通过找到到达他家的最佳路线来最大程度地提高你的胜算。这是你在笔记本电脑上找到的地图。

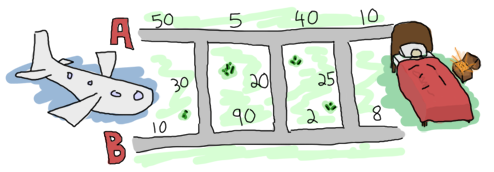
在阅读在线书籍后成为 Erlang 的忠实粉丝后，你决定使用该语言来解决这个问题。为了便于处理地图，你以以下方式将数据输入名为 road.txt 的文件中。

50
10
30
5
90
20
40
2
25
10
8
0

道路的布局模式为：A1, B1, X1, A2, B2, X2, ..., An, Bn, Xn，其中 X 是连接地图 A 侧和 B 侧的其中一条道路。我们插入一个 0 作为最后一个 X 段，因为无论我们做什么，我们都已经到达目的地了。数据可能以 {A,B,X} 形式的 3 元素元组（三元组）的形式组织。

接下来你意识到，当你不知道如何手动解决这个问题时，用 Erlang 来解决这个问题毫无意义。为了做到这一点，我们将利用递归教会我们的知识。

在编写递归函数时，第一步是要找到我们的基本情况。对于我们手头的这个问题，这将是如果我们只有一个元组要分析，也就是说，如果我们只需要在 A、B（以及穿过 X，在这种情况下，这是无用的，因为我们已经在目的地）之间做出选择。

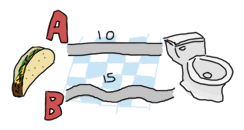
那么，选择就只有在选择路径 A 或路径 B 哪个最短之间。如果你已经正确地学习了递归，你就会知道我们应该尝试收敛到基本情况。这意味着，在每一步中，我们都希望将问题简化为在下一步中在 A 和 B 之间进行选择。

让我们扩展我们的地图并重新开始。

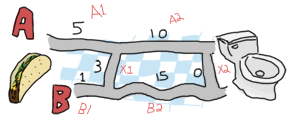
啊！变得有趣了！我们如何将三元组 {5,1,3} 简化为在 A 和 B 之间的严格选择？让我们看看 A 有多少种可能的选项。要到达 A1 和 A2 的交点（我称之为点 A1），我可以直接走 A1 路线 (5)，或者从 B1 (1) 来，然后穿过 X1 (3)。在这种情况下，第一个选项 (5) 比第二个选项 (4) 更长。对于选项 A，最短路径是 [B, X]。那么 B 有什么选项呢？你可以从 A1 (5) 继续前进，然后穿过 X1 (3)，或者严格地走 B1 (1) 路线。

好吧！我们得到的是一条长度为 4 的路径 [B, X] 朝向第一个交叉点 A，以及一条长度为 1 的路径 [B] 朝向 B1 和 B2 的交叉点。然后，我们必须决定是在前往第二个点 A（A2 和端点或 X2 的交点）还是第二个点 B（B2 和 X2 的交点）之间进行选择。为了做出决定，我建议我们像以前一样做。现在你除了服从我之外别无选择，因为我是写这篇文章的人。开始吧！

在这种情况下可以采取的所有可能路径都可以像以前一样找到。我们可以通过以下两种方式到达下一个点 A：从 [B, X] 走 A2 路线，这将使我们得到长度为 14 的路径 (14 = 4 + 10)，或者从 [B] 走 B2，然后走 X2，这将使我们得到长度为 16 的路径 (16 = 1 + 15 + 0)。在这种情况下，路径 [B, X, A] 比 [B, B, X] 更好。

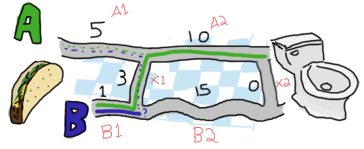
我们还可以通过以下两种方式到达下一个点 B：从 [B, X] 走 A2 路线，然后穿过 X2，长度为 14 (14 = 4 + 10 + 0)，或者从 [B] 走 B2 路线，长度为 16 (16 = 1 + 15)。在这里，最佳路径是选择第一个选项，[B, X, A, X]。

因此，当整个过程完成时，我们剩下两条路径，A 或 B，长度均为 14。它们中的任何一个都是正确的。考虑到最后一个 X 段的长度为 0，所以最后的选择始终会有两条长度相同的路径。通过递归地解决我们的问题，我们确保了始终能够在最后获得最短路径。还不错吧？

巧妙的是，我们已经给自己提供了构建递归函数所需的基本逻辑部分。你可以根据需要实现它，但我承诺我们将自己编写很少的递归函数。我们将使用 fold。

那么，我们到哪里了呢？啊，是的！我们准备好了要作为输入提供给它的文件。要进行文件操作，file 模块 是我们最好的工具。它包含许多适用于许多编程语言的常见函数，用于处理文件本身（设置权限、移动文件、重命名和删除文件等）。

它还包含用于从文件读取和/或写入文件的常见函数，例如：file:open/2 和 file:close/1 用于执行它们的名称所指示的操作（打开和关闭文件！），file:read/2 用于获取文件的内容（作为字符串或二进制文件），file:read_line/1 用于读取单行，file:position/3 用于将打开文件的指针移动到给定位置等。

其中还包含许多快捷函数，例如 file:read_file/1（打开并以二进制形式读取内容），file:consult/1（打开并以 Erlang 术语解析文件）或 file:pread/2（更改位置，然后读取）和 pwrite/2（更改位置并写入内容）。

有了所有这些选择，找到一个函数来读取我们的 road.txt 文件将会很容易。由于我们知道我们的道路相对较小，我们将调用 file:read_file("road.txt").'。

1> {ok, Binary} = file:read_file("road.txt").
{ok,<<"50\r\n10\r\n30\r\n5\r\n90\r\n20\r\n40\r\n2\r\n25\r\n10\r\n8\r\n0\r\n">>}
2> S = string:tokens(binary_to_list(Binary), "\r\n\t ").
["50","10","30","5","90","20","40","2","25","10","8","0"]

请注意，在这种情况下，我在有效标记中添加了一个空格 (" ") 和一个制表符 ("\t")，以便文件可以以 "50 10 30 5 90 20 40 2 25 10 8 0" 的形式编写。鉴于该列表，我们需要将字符串转换为整数。我们将使用与我们在 RPN 计算器中使用的方法类似的方法。

3> [list_to_integer(X) || X <- S].
[50,10,30,5,90,20,40,2,25,10,8,0]

让我们开始一个名为 road.erl 的新模块，并将此逻辑写下来。

-module(road).
-compile(export_all).

main() ->
    File = "road.txt",
    {ok, Bin} = file:read_file(File),
    parse_map(Bin).

parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")].

函数 main/0 负责读取文件的内容并将它传递给 parse_map/1。由于我们使用函数 file:read_file/1 从 road.txt 中获取内容，因此我们获得的结果是一个二进制文件。为此，我让函数 parse_map/1 同时匹配列表和二进制文件。在二进制文件的情况下，我们只需使用将字符串转换为列表后的字符串再次调用该函数（我们用于分割字符串的函数仅适用于列表）。

解析地图的下一步是将数据重新组合成前面描述的 {A,B,X} 形式。不幸的是，没有简单的通用方法可以一次从列表中提取 3 个元素，因此我们将不得不使用递归函数来进行模式匹配以实现它。

group_vals([], Acc) ->
    lists:reverse(Acc);
group_vals([A,B,X|Rest], Acc) ->
    group_vals(Rest, [{A,B,X} | Acc]).

该函数以标准的尾递归方式工作；这里没有太复杂的操作。我们只需要修改 parse_map/1 来调用它即可。

parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    Values = [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")],
    group_vals(Values, []).

如果我们尝试编译所有内容，我们现在应该有一个有意义的道路。

1> c(road).
{ok,road}
2> road:main().
[{50,10,30},{5,90,20},{40,2,25},{10,8,0}]

啊，是的，看起来没错。我们得到了编写函数所需的块，该函数将适合 fold。为了使这能够正常工作，找到一个合适的累加器是必要的。

为了决定使用什么作为累加器，我发现最容易使用的方法是想象自己在算法运行过程中的中间。对于这个特定问题，我将想象自己正在尝试找到第二个三元组 ({5,90,20}) 的最短路径。为了决定哪条路径是最好的，我需要有上一个三元组的结果。幸运的是，我们知道如何做，因为我们不需要累加器，并且已经获得了所有这些逻辑。所以对于 A

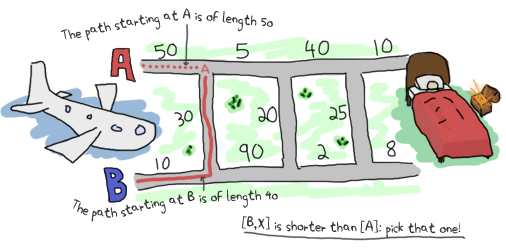
并取这两个路径中最短的路径。对于 B，情况类似。

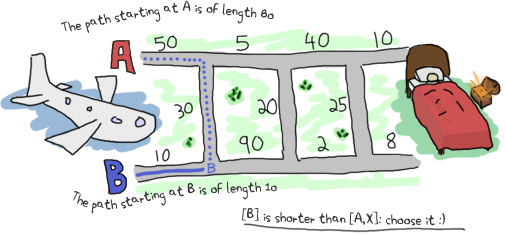
因此，现在我们知道来自 A 的当前最佳路径是 [B, X]。我们还知道它的长度为 40。对于 B，路径 simply [B]，长度为 10。我们可以使用这些信息通过重新应用相同的逻辑来找到 A 和 B 的下一个最佳路径，但在表达式中计算之前的路径。我们需要的其他数据是行进的路径，以便我们可以将其显示给用户。鉴于我们需要两条路径（一条用于 A，一条用于 B）和两个累积的长度，我们的累加器可以采用 {{DistanceA, PathA}, {DistanceB, PathB}} 的形式。这样，fold 的每次迭代都可以访问所有状态，并且我们构建它，以便最终将其显示给用户。

这为我们的函数提供了所有必要的参数：{A,B,X} 三元组和 {{DistanceA,PathA}, {DistanceB,PathB}} 形式的累加器。

为了获得累加器，可以用以下方式将它写成代码

shortest_step({A,B,X}, {{DistA,PathA}, {DistB,PathB}}) ->
    OptA1 = {DistA + A, [{a,A}|PathA]},
    OptA2 = {DistB + B + X, [{x,X}, {b,B}|PathB]},
    OptB1 = {DistB + B, [{b,B}|PathB]},
    OptB2 = {DistA + A + X, [{x,X}, {a,A}|PathA]},
    {erlang:min(OptA1, OptA2), erlang:min(OptB1, OptB2)}.

这里，OptA1 获取 A 的第一个选项（通过 A 走），OptA2 获取第二个选项（通过 B 走，然后走 X）。变量 OptB1 和 OptB2 对点 B 进行类似的处理。最后，我们返回带有获得的路径的累加器。

关于上面代码中保存的路径，请注意，我决定使用 [{x,X}] 形式而不是 [x] 形式，因为这样对用户来说可能很方便，因为他可以知道每个段的长度。我做的另一件事是，我反向累积路径 ({x,X} 在 {b,B} 之前)。这是因为我们处于 fold 中，fold 是尾递归的：整个列表被反转，因此有必要将最后一个遍历的元素放在其他元素之前。

最后，我使用 erlang:min/2 来查找最短路径。在元组上使用这样的比较函数听起来可能很奇怪，但请记住，每个 Erlang 术语都可以与任何其他术语进行比较！因为长度是元组的第一个元素，所以我们可以用这种方式对它们进行排序。

剩下的就是将该函数放到 fold 中。

optimal_path(Map) ->
    {A,B} = lists:foldl(fun shortest_step/2, {{0,[]}, {0,[]}}, Map),
    {_Dist,Path} = if hd(element(2,A)) =/= {x,0} -> A;
                      hd(element(2,B)) =/= {x,0} -> B
                   end,
    lists:reverse(Path).

在 fold 结束时，两条路径的距离应该相同，只是其中一条路径会经过最终的 {x,0} 段。if 会查看两条路径中最后访问的元素，并返回不经过 {x,0} 的那条路径。选择步骤最少的路径（与 length/1 进行比较）也可以。一旦选择了最短的路径，它就会被反转（它以尾递归方式构建；你必须反转它）。然后，你可以将其显示给世界，或者将其保密，并获得你富有的叔叔的遗产。为此，你必须修改主函数以调用 optimal_path/1。然后它可以被编译。

main() ->
    File = "road.txt",
    {ok, Bin} = file:read_file(File),
    optimal_path(parse_map(Bin)).

哦，看！我们得到了正确答案！干得好！

1> c(road).
{ok,road}
2> road:main().
[{b,10},{x,30},{a,5},{x,20},{b,2},{b,8}]

或者，以一种直观的方式来说

但是你知道什么会真正有用吗？能够从 Erlang shell 外部运行我们的程序。我们需要再次更改我们的主函数

main([FileName]) ->
    {ok, Bin} = file:read_file(FileName),
    Map = parse_map(Bin),
    io:format("~p~n",[optimal_path(Map)]),
    erlang:halt().

主函数现在具有 1 的元数，需要从命令行接收参数。我还添加了函数 erlang:halt/0，它将在被调用后关闭 Erlang VM。我还将对 optimal_path/1 的调用包装在 io:format/2 中，因为这是让文本在 Erlang shell 外部可见的唯一方法。

有了所有这些，你的 road.erl 文件现在应该看起来像这样（减去注释）

-module(road).
-compile(export_all).

main([FileName]) ->
    {ok, Bin} = file:read_file(FileName),
    Map = parse_map(Bin),
    io:format("~p~n",[optimal_path(Map)]),
    erlang:halt(0).

%% Transform a string into a readable map of triples
parse_map(Bin) when is_binary(Bin) ->
    parse_map(binary_to_list(Bin));
parse_map(Str) when is_list(Str) ->
    Values = [list_to_integer(X) || X <- string:tokens(Str,"\r\n\t ")],
    group_vals(Values, []).

group_vals([], Acc) ->
    lists:reverse(Acc);
group_vals([A,B,X|Rest], Acc) ->
    group_vals(Rest, [{A,B,X} | Acc]).

%% Picks the best of all paths, woo!
optimal_path(Map) ->
    {A,B} = lists:foldl(fun shortest_step/2, {{0,[]}, {0,[]}}, Map),
    {_Dist,Path} = if hd(element(2,A)) =/= {x,0} -> A;
                      hd(element(2,B)) =/= {x,0} -> B
                   end,
    lists:reverse(Path).

%% actual problem solving
%% change triples of the form {A,B,X}
%% where A,B,X are distances and a,b,x are possible paths
%% to the form {DistanceSum, PathList}.
shortest_step({A,B,X}, {{DistA,PathA}, {DistB,PathB}}) ->
    OptA1 = {DistA + A, [{a,A}|PathA]},
    OptA2 = {DistB + B + X, [{x,X}, {b,B}|PathB]},
    OptB1 = {DistB + B, [{b,B}|PathB]},
    OptB2 = {DistA + A + X, [{x,X}, {a,A}|PathA]},
    {erlang:min(OptA1, OptA2), erlang:min(OptB1, OptB2)}.

并运行代码

$ erlc road.erl
$ erl -noshell -run road main road.txt
[{b,10},{x,30},{a,5},{x,20},{b,2},{b,8}]

没错，就是它！这几乎是你让它工作所需做的全部工作。你可以为自己创建一个 bash/批处理文件，将该行包装成一个可执行文件，或者你可以查看 escript 以获得类似的结果。

正如我们在这两个练习中所见，当你将问题分解成小的部分并分别解决它们，然后再将它们拼凑起来时，解决问题会容易得多。在不理解的情况下就去编程也是没有意义的。最后，一些测试总是受欢迎的。它们可以让你确保一切正常，并允许你在不改变结果的情况下更改代码。

• < 上一页
• 索引
• 下一页 >

除非另有说明，否则本网站上的内容均根据知识共享署名非商业性禁止演绎许可协议进行许可