递归
你好，递归！
一些习惯了命令式和面向对象编程语言的读者可能想知道为什么还没有展示循环。答案是“循环是什么？” 事实上，函数式编程语言通常不提供像 for 和 while 这样的循环结构。相反，函数式程序员依靠一个名为递归的愚蠢概念。
我想您还记得在介绍章节中是如何解释不变变量的。如果您不记得，您可以 重新学习一下！递归也可以借助数学概念和函数来解释。像阶乘这样的基本数学函数就是一个可以递归表达的函数的很好的例子。一个数 n 的阶乘是序列 1 x 2 x 3 x ... x n 的乘积，或者换句话说，是 n x (n-1) x (n-2) x ... x 1。举几个例子，3 的阶乘是 3! = 3 x 2 x 1 = 6。4 的阶乘是 4! = 4 x 3 x 2 x 1 = 24。这样的函数可以用下面的数学符号表示
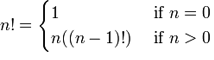
这告诉我们，如果我们得到的 n 值是 0，我们将返回结果 1。对于任何大于 0 的值，我们返回 n 乘以 n-1 的阶乘，它会一直展开直到达到 1
4! = 4 x 3! 4! = 4 x 3 x 2! 4! = 4 x 3 x 2 x 1! 4! = 4 x 3 x 2 x 1 x 1
如何在 Erlang 中将这样的函数从数学符号转换为代码？转换很简单。看一下符号的各个部分：n!、1 和 n((n-1)!) 以及 if 语句。我们这里得到的是一个函数名 (n!)、保护语句 (if 语句) 和函数体 (1 和 n((n-1)!))。我们将 n! 重命名为 fac(N) 以限制我们的语法，然后得到以下结果
-module(recursive). -export([fac/1]). fac(N) when N == 0 -> 1; fac(N) when N > 0 -> N*fac(N-1).
现在这个阶乘函数就完成了！它与数学定义非常相似，真的。借助模式匹配，我们可以简化定义
fac(0) -> 1; fac(N) when N > 0 -> N*fac(N-1).
所以，对于一些本质上是递归的数学定义来说，这既简单又快捷。我们循环了！可以简短地将递归定义为“一个调用自身的函数”。但是，我们需要有一个停止条件（真正的术语是基本情况），因为否则我们将无限循环。在我们的例子中，停止条件是当 n 等于 0 时。此时，我们不再告诉我们的函数调用自身，它会立即停止执行。
长度
让我们尝试使其更实用一点。我们将实现一个函数来计算列表包含多少个元素。所以我们从一开始就知道我们需要
- 一个基本情况；
- 一个调用自身的函数；
- 一个用于尝试我们函数的列表。
对于大多数递归函数，我发现基本情况更容易先写：我们可以拥有的最简单的输入是什么来找到长度？当然，空列表是最简单的，长度为 0。所以让我们记住，在处理长度时，[] = 0。那么下一个最简单的列表长度为 1：[_] = 1。这听起来足以让我们开始定义。我们可以把它写下来
len([]) -> 0; len([_]) -> 1.
太棒了！我们可以计算列表的长度，前提是长度是 0 或 1！确实非常有用。当然，它毫无用处，因为它还没有递归，这让我们来到了最难的部分：扩展我们的函数，使其可以调用自身以处理长度大于 1 或 0 的列表。之前 提到过，列表被递归定义为 [1 | [2| ... [n | []]]]。这意味着我们可以使用 [H|T] 模式匹配一个或多个元素的列表，因为长度为一的列表将被定义为 [X|[]]，长度为二的列表将被定义为 [X|[Y|[]]]。请注意，第二个元素本身就是一个列表。这意味着我们只需要计算第一个元素，函数可以调用自身处理第二个元素。考虑到列表中的每个值都算作长度为 1，所以函数可以按照以下方式重写
len([]) -> 0; len([_|T]) -> 1 + len(T).
现在您有了自己的递归函数来计算列表的长度。为了查看 len/1 在运行时的行为，让我们在一个给定的列表上试用它，比如 [1,2,3,4]
len([1,2,3,4]) = len([1 | [2,3,4])
= 1 + len([2 | [3,4]])
= 1 + 1 + len([3 | [4]])
= 1 + 1 + 1 + len([4 | []])
= 1 + 1 + 1 + 1 + len([])
= 1 + 1 + 1 + 1 + 0
= 1 + 1 + 1 + 1
= 1 + 1 + 2
= 1 + 3
= 4
这就是正确答案。恭喜您在 Erlang 中写出了第一个有用的递归函数！
尾递归的长度
您可能已经注意到，对于一个包含 4 个元素的列表，我们将函数调用扩展成一条包含 5 个加法的链。虽然这对于短列表来说可以正常工作，但如果您的列表包含数百万个值，就会出现问题。您不希望为了这样一个简单的计算而在内存中保留数百万个数字。这是浪费的，而且有更好的方法。这就是尾递归的用武之地。
尾递归是一种将上述线性过程（它随着元素数量的增加而增长）转换为迭代过程（实际上没有增长）的方法。为了使函数调用成为尾递归，它需要“单独存在”。让我解释一下：我们之前的调用之所以会增长，是因为第一部分的答案依赖于第二部分的评估。1 + len(Rest) 的答案需要找到 len(Rest) 的答案。然后，函数 len(Rest) 本身需要找到另一个函数调用的结果。加法会一直累积，直到找到最后一个加法，只有到那时才会计算最终结果。尾递归旨在通过在计算过程中减少操作来消除这种操作的累积。
为了实现这一点，我们需要在函数中保存一个额外的临时变量作为参数。我将借助阶乘函数来说明这个概念，但这次我们将把它定义为尾递归。前面提到的临时变量有时被称为累加器，它充当一个地方，用于存储我们计算结果，以便在计算过程中限制调用的增长
tail_fac(N) -> tail_fac(N,1). tail_fac(0,Acc) -> Acc; tail_fac(N,Acc) when N > 0 -> tail_fac(N-1,N*Acc).
在这里，我定义了 tail_fac/1 和 tail_fac/2。这样做的原因是 Erlang 不允许函数中使用默认参数（不同的元数意味着不同的函数），所以我们手动执行。在这种情况下，tail_fac/1 充当尾递归 tail_fac/2 函数的抽象。tail_fac/2 的隐藏累加器的细节无关紧要，因此我们只会在模块中导出 tail_fac/1。运行此函数时，我们可以将其扩展为
tail_fac(4) = tail_fac(4,1) tail_fac(4,1) = tail_fac(4-1, 4*1) tail_fac(3,4) = tail_fac(3-1, 3*4) tail_fac(2,12) = tail_fac(2-1, 2*12) tail_fac(1,24) = tail_fac(1-1, 1*24) tail_fac(0,24) = 24
看到了区别吗？现在我们永远不需要在内存中保存超过两个元素：空间使用量是恒定的。计算 4 的阶乘所需的内存空间与计算 100 万的阶乘所需的内存空间一样（如果我们忘记 4! 在其完整表示中比 1M! 小，那就是了）。
有了尾递归阶乘的例子，您可能能够看到如何将这种模式应用于我们的 len/1 函数。我们需要做的就是使我们的递归调用“单独存在”。如果您喜欢直观的例子，想象一下，您将通过添加参数将 +1 部分放在函数调用中
len([]) -> 0; len([_|T]) -> 1 + len(T).
变为
tail_len(L) -> tail_len(L,0). tail_len([], Acc) -> Acc; tail_len([_|T], Acc) -> tail_len(T,Acc+1).
现在您的长度函数是尾递归的。
更多递归函数
我们将再写几个递归函数，以便更习惯一点。毕竟，递归是 Erlang 中唯一存在的循环结构（除了列表推导），它是最重要的概念之一。它在您之后尝试的任何其他函数式编程语言中也很有用，所以请记笔记！
我们将要写的第一个函数是 duplicate/2。此函数以一个整数作为第一个参数，然后以任何其他项作为第二个参数。然后，它将创建一个包含指定整数个项的副本的列表。和之前一样，首先考虑基本情况可能有助于您开始。对于 duplicate/2，要求重复某项 0 次是最基本的操作。我们只需要返回一个空列表，无论该项是什么。其他任何情况都需要尝试通过调用自身来达到基本情况。我们还将禁止整数取负值，因为您不能将某项重复 -n 次
duplicate(0,_) ->
[];
duplicate(N,Term) when N > 0 ->
[Term|duplicate(N-1,Term)].
找到基本的递归函数后，将它转换为尾递归函数就变得更容易，方法是将列表构建移到一个临时变量中
tail_duplicate(N,Term) ->
tail_duplicate(N,Term,[]).
tail_duplicate(0,_,List) ->
List;
tail_duplicate(N,Term,List) when N > 0 ->
tail_duplicate(N-1, Term, [Term|List]).
成功！我想在这里改变一下话题，在尾递归和 while 循环之间建立一个联系。我们的 tail_duplicate/2 函数具有 while 循环的所有常见部分。如果我们想象一个具有 Erlang 类语法的虚构语言中的 while 循环，我们的函数看起来可能会像这样
function(N, Term) ->
while N > 0 ->
List = [Term|List],
N = N-1
end,
List.
请注意，虚构语言和 Erlang 中的所有元素都存在。只有它们的位置发生了变化。这表明，一个正确的尾递归函数类似于一个迭代过程，就像 while 循环。
当我们通过编写一个 reverse/1 函数来比较递归函数和尾递归函数时，我们还可以“发现”一个有趣的特性，该函数将反转一个项列表。对于这样的函数，基本情况是一个空列表，因为我们没有什么要反转的。在这种情况下，我们只需要返回一个空列表。其他任何可能性都应该尝试通过调用自身来收敛到基本情况，就像 duplicate/2 一样。我们的函数将通过模式匹配 [H|T] 遍历列表，然后将 H 放置在列表的剩余部分之后
reverse([]) -> []; reverse([H|T]) -> reverse(T)++[H].
在长列表上，这将是一场真正的噩梦：我们不仅要堆叠所有追加操作，而且还需要遍历整个列表才能进行每次追加，直到最后一次！对于视觉读者来说，许多检查可以表示为
reverse([1,2,3,4]) = [4]++[3]++[2]++[1]
↑ ↵
= [4,3]++[2]++[1]
↑ ↑ ↵
= [4,3,2]++[1]
↑ ↑ ↑ ↵
= [4,3,2,1]
这就是尾递归发挥作用的地方。因为我们将使用一个累加器，并在每次追加时向其中添加一个新的头部，所以我们的列表将自动反转。让我们首先看看实现
tail_reverse(L) -> tail_reverse(L,[]). tail_reverse([],Acc) -> Acc; tail_reverse([H|T],Acc) -> tail_reverse(T, [H|Acc]).
如果我们以与普通版本类似的方式表示它，我们会得到
tail_reverse([1,2,3,4]) = tail_reverse([2,3,4], [1])
= tail_reverse([3,4], [2,1])
= tail_reverse([4], [3,2,1])
= tail_reverse([], [4,3,2,1])
= [4,3,2,1]
这表明，为了反转列表而访问的元素数量现在是线性的：我们不仅避免了堆栈的增长，而且还以更有效的方式执行了操作！
另一个可以实现的函数是 sublist/2，它接收一个列表 L 和一个整数 N，并返回列表的前 N 个元素。例如，sublist([1,2,3,4,5,6],3) 将返回 [1,2,3]。再次，基本情况是尝试从一个列表中获取 0 个元素。但是请注意，sublist/2 有点不同。当传递的列表为空时，您有一个第二个基本情况！如果我们不检查空列表，则在调用 recursive:sublist([1],2). 时会抛出错误，而我们希望得到 [1]。一旦定义了这一点，函数的递归部分只需要遍历列表，保留元素，直到它遇到其中一个基本情况
sublist(_,0) -> []; sublist([],_) -> []; sublist([H|T],N) when N > 0 -> [H|sublist(T,N-1)].
然后可以像以前一样将其转换为尾递归形式
tail_sublist(L, N) -> tail_sublist(L, N, []).
tail_sublist(_, 0, SubList) -> SubList;
tail_sublist([], _, SubList) -> SubList;
tail_sublist([H|T], N, SubList) when N > 0 ->
tail_sublist(T, N-1, [H|SubList]).
这个函数有一个缺陷。一个致命的缺陷！ 我们以与反转列表时完全相同的方式使用列表作为累加器。如果按原样编译此函数，sublist([1,2,3,4,5,6],3) 不会返回 [1,2,3]，而是 [3,2,1]。我们能做的唯一事情是获取最终结果并自己反转它。只需更改 tail_sublist/2 调用并保持所有递归逻辑不变。
tail_sublist(L, N) -> reverse(tail_sublist(L, N, [])).
最终结果将按正确顺序排列。在尾递归调用后反转列表似乎是一种浪费时间的行为，你部分是对的（我们仍然可以通过这样做来节省内存）。在较短的列表中，你可能会发现你的代码在使用普通递归调用时比使用尾递归调用运行得更快，但随着数据集的增长，反转列表将相对轻量级。
注意： 而不是编写你自己的 reverse/1 函数，你应该使用 lists:reverse/1。它被用于尾递归调用如此之多，以至于 Erlang 的维护者和开发人员决定将其变成一个 BIF。你的列表现在可以从极快的反转中获益（感谢用 C 编写的函数），这将使反转的缺点不那么明显。本章中的其余代码将使用我们自己的反转函数，但之后你不应该再使用它。
为了更进一步，我们将编写一个压缩函数。压缩函数将接受两个长度相同的列表作为参数，并将它们连接成一个包含两个项的元组列表。我们自己的 zip/2 函数将以这种方式工作。
1> recursive:zip([a,b,c],[1,2,3]).
[{a,1},{b,2},{c,3}]
鉴于我们希望我们的参数都具有相同的长度，基本情况将是压缩两个空列表。
zip([],[]) -> [];
zip([X|Xs],[Y|Ys]) -> [{X,Y}|zip(Xs,Ys)].
但是，如果你想要一个更宽松的压缩函数，你可以决定在两个列表中的任何一个完成时结束。在这种情况下，因此你有两个基本情况。
lenient_zip([],_) -> [];
lenient_zip(_,[]) -> [];
lenient_zip([X|Xs],[Y|Ys]) -> [{X,Y}|lenient_zip(Xs,Ys)].
请注意，无论我们的基本情况是什么，函数的递归部分都保持不变。我建议你尝试自己制作 zip/2 和 lenient_zip/2 的尾递归版本，以确保你完全理解如何制作尾递归函数：它们将是大型应用程序的核心概念之一，我们的主循环将以此方式构建。
如果你想检查你的答案，请查看我的 recursive.erl 实现，更准确地说是 tail_zip/2 和 tail_lenient_zip/3 函数。
注意： 在这里看到的尾递归不会使内存增长，因为当虚拟机看到一个函数在尾部位置（函数中要评估的最后一个表达式）调用自身时，它会消除当前的堆栈帧。这被称为尾调用优化 (TCO)，它是更一般的优化称为最后调用优化 (LCO) 的特例。
当函数体中要评估的最后一个表达式是另一个函数调用时，就会进行 LCO。当发生这种情况时，与 TCO 一样，Erlang VM 会避免存储堆栈帧。因此，尾递归也可能发生在多个函数之间。例如，函数链 a() -> b(). b() -> c(). c() -> a(). 将有效地创建一个无限循环，该循环不会耗尽内存，因为 LCO 避免了堆栈溢出。这个原则，加上我们对累加器的使用，是尾递归有用的原因。
快速，排序！
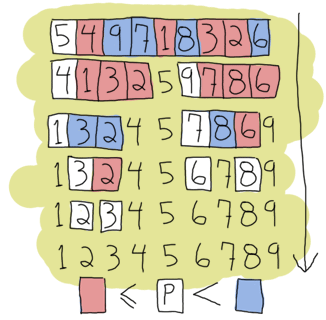
我现在可以（并且将）假设递归和尾递归对你来说是有意义的，但为了确保，我将推动一个更复杂的例子，快速排序。是的，传统的“嘿，看看我可以编写简短的功能代码”典型例子。快速排序的简单实现方法是取列表的第一个元素，即枢轴，然后将所有小于或等于枢轴的元素放在一个新列表中，并将所有大于枢轴的元素放在另一个列表中。然后，我们取每个列表并对它们进行相同的操作，直到每个列表越来越小。这会一直持续下去，直到你只剩下一个空列表需要排序，这将是我们的基本情况。这种实现被称为简单，因为更智能的快速排序版本将尝试选择最佳的枢轴以更快地排序。但是，对于我们的示例，我们并不关心这些。
为此，我们需要两个函数：第一个函数将列表划分为较小和较大部分，第二个函数将划分函数应用于每个新列表，并将它们粘合在一起。首先，我们将编写粘合函数。
quicksort([]) -> [];
quicksort([Pivot|Rest]) ->
{Smaller, Larger} = partition(Pivot,Rest,[],[]),
quicksort(Smaller) ++ [Pivot] ++ quicksort(Larger).
这显示了基本情况，一个列表已经通过另一个函数划分为更大更小的部分，使用枢轴，将两个快速排序的列表附加到它的前面和后面。因此，这应该负责组装列表。现在是划分函数。
partition(_,[], Smaller, Larger) -> {Smaller, Larger};
partition(Pivot, [H|T], Smaller, Larger) ->
if H =< Pivot -> partition(Pivot, T, [H|Smaller], Larger);
H > Pivot -> partition(Pivot, T, Smaller, [H|Larger])
end.
你现在可以运行你的快速排序函数。如果你之前在互联网上查找过 Erlang 示例，你可能已经看到快速排序的另一种实现，它更简单，更容易阅读，但使用了列表推导。易于替换的部分是那些创建新列表的部分，partition/4 函数。
lc_quicksort([]) -> [];
lc_quicksort([Pivot|Rest]) ->
lc_quicksort([Smaller || Smaller <- Rest, Smaller =< Pivot])
++ [Pivot] ++
lc_quicksort([Larger || Larger <- Rest, Larger > Pivot]).
主要区别在于此版本更容易阅读，但作为交换，它必须遍历列表两次才能将其划分为两个部分。这是一场清晰度与性能的较量，但真正的输家是你，因为一个函数 lists:sort/1 已经存在。使用那个而不是这个。
不要喝太多酷爱
所有这些简洁性对于教育目的很好，但不适合性能。许多函数式编程教程从未提到这一点！首先，这里的所有实现都需要多次处理等于枢轴的值。我们可以决定改为返回 3 个列表：更小、更大、等于枢轴的元素，以使其更高效。
另一个问题与我们如何在将分区列表附加到枢轴时需要多次遍历它们有关。通过在将列表划分为三个部分时进行连接，可以稍微减少开销。如果你对此感到好奇，请查看 recursive.erl 中的最后一个函数 (bestest_qsort/1) 作为示例。
所有这些快速排序的一个很好的点是它们将适用于你拥有的任何数据类型的列表，即使是列表的元组等等。尝试一下，它们可以工作！
不仅仅是列表
通过阅读本章，你可能开始认为 Erlang 中的递归主要是与列表有关的事情。虽然列表是递归定义的数据结构的一个很好的例子，但肯定不止这些。为了多样性，我们将了解如何构建二叉树，然后从它们中读取数据。
首先，重要的是要定义什么是树。在我们的例子中，它是从上到下所有的节点。节点是包含键、与键关联的值以及另外两个节点的元组。在这两个节点中，我们需要一个比包含它们的节点具有更小键的节点，另一个具有更大键的节点。所以这就是递归！树是一个包含节点的节点，每个节点都包含节点，这些节点依次也包含节点。这不能一直持续下去（我们没有无限的数据来存储），因此我们将说我们的节点也可以包含空节点。
为了表示节点，元组是合适的数据结构。对于我们的实现，我们可以将这些元组定义为 {node, {Key, Value, Smaller, Larger}}（一个带标签的元组！），其中 Smaller 和 Larger 可以是另一个类似的节点或一个空节点 ({node, nil})。我们实际上不需要比这更复杂的概念。
让我们开始构建一个模块，用于我们的 非常基本的树实现。第一个函数 empty/0 返回一个空节点。空节点是新树的起点，也称为根。
-module(tree).
-export([empty/0, insert/3, lookup/2]).
empty() -> {node, 'nil'}.
通过使用该函数，然后以相同的方式封装所有节点的表示形式，我们隐藏了树的实现，因此人们不需要知道它是如何构建的。所有这些信息都可以由模块单独包含。如果你决定更改节点的表示形式，那么你可以这样做，而不会破坏外部代码。
要向树中添加内容，我们必须首先了解如何递归地遍历它。让我们以与之前所有其他递归示例相同的方式进行，尝试找到基本情况。鉴于空树是一个空节点，因此我们的基本情况逻辑上是一个空节点。因此，每当我们遇到空节点时，那就是我们可以添加新键/值的地方。在其他情况下，我们的代码必须遍历树以尝试找到一个可以放置内容的空节点。
要从根开始找到一个空节点，我们必须使用以下事实：Smaller 和 Larger 节点的存在让我们可以通过将我们要插入的新键与当前节点的键进行比较来导航。如果新键小于当前节点的键，我们尝试在 Smaller 内部找到空节点，如果新键更大，则在 Larger 内部找到空节点。但是，还有一种情况：如果新键等于当前节点的键怎么办？我们有两个选择：让程序失败或用新值替换旧值。这是我们将在这里采用的选项。将所有这些逻辑放入函数中，其工作方式如下。
insert(Key, Val, {node, 'nil'}) ->
{node, {Key, Val, {node, 'nil'}, {node, 'nil'}}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey < Key ->
{node, {Key, Val, insert(NewKey, NewVal, Smaller), Larger}};
insert(NewKey, NewVal, {node, {Key, Val, Smaller, Larger}}) when NewKey > Key ->
{node, {Key, Val, Smaller, insert(NewKey, NewVal, Larger)}};
insert(Key, Val, {node, {Key, _, Smaller, Larger}}) ->
{node, {Key, Val, Smaller, Larger}}.
请注意，此函数返回一棵全新的树。这是函数式语言仅具有单一赋值的典型特征。虽然这可以被认为是低效的，但两棵树的两个版本的许多底层结构有时恰好是相同的，因此它们是共享的，只有在需要时才由 VM 复制。
在这个示例树实现中剩下要做的事情是创建一个 lookup/2 函数，该函数将允许你通过提供其键来从树中找到一个值。所需的逻辑与用于向树中添加新内容的逻辑极其相似：我们逐步遍历节点，检查查找键是否等于、小于或大于当前节点的键。我们有两个基本情况：一个是在节点为空时（键不在树中），另一个是在找到键时。因为我们不希望我们的程序每次查找不存在的键时都崩溃，所以我们将返回原子 'undefined'。否则，我们将返回 {ok, Value}。这样做的原因是，如果我们只返回 Value，并且节点包含原子 'undefined'，我们将无法知道树是否返回了正确的值或未能找到它。通过将成功的情况包装在这样的元组中，我们使理解哪一个是哪一个变得容易。以下是实现的函数。
lookup(_, {node, 'nil'}) ->
undefined;
lookup(Key, {node, {Key, Val, _, _}}) ->
{ok, Val};
lookup(Key, {node, {NodeKey, _, Smaller, _}}) when Key < NodeKey ->
lookup(Key, Smaller);
lookup(Key, {node, {_, _, _, Larger}}) ->
lookup(Key, Larger).
我们完成了。让我们通过创建一个小的电子邮件地址簿来测试它。编译文件并启动 shell。
1> T1 = tree:insert("Jim Woodland", "[email protected]", tree:empty()).
{node,{"Jim Woodland","[email protected]",
{node,nil},
{node,nil}}}
2> T2 = tree:insert("Mark Anderson", "[email protected]", T1).
{node,{"Jim Woodland","[email protected]",
{node,nil},
{node,{"Mark Anderson","[email protected]",
{node,nil},
{node,nil}}}}}
3> Addresses = tree:insert("Anita Bath", "[email protected]", tree:insert("Kevin Robert", "[email protected]", tree:insert("Wilson Longbrow", "[email protected]", T2))).
{node,{"Jim Woodland","[email protected]",
{node,{"Anita Bath","[email protected]",
{node,nil},
{node,nil}}},
{node,{"Mark Anderson","[email protected]",
{node,{"Kevin Robert","[email protected]",
{node,nil},
{node,nil}}},
{node,{"Wilson Longbrow","[email protected]",
{node,nil},
{node,nil}}}}}}}
现在你可以使用它查找电子邮件地址。
4> tree:lookup("Anita Bath", Addresses).
{ok, "[email protected]"}
5> tree:lookup("Jacques Requin", Addresses).
undefined
这结束了我们从除列表之外的递归数据结构构建的功能地址簿示例！Anita Bath 现在...
注意： 我们的树实现非常简单：不支持删除节点或重新平衡树以加快后续查找等常见操作。如果您有兴趣实现和/或探索这些操作，建议研究 Erlang 的 `gb_trees` 模块（`otp_src_R<version>B<revision>/lib/stdlib/src/gb_trees.erl`）的实现。这也是您在代码中处理树时应该使用的模块，而不是重新造轮子。
递归思考
如果您已经理解了本章中的所有内容，递归思考可能已经变得更加直观。与命令式对应物（通常在 while 或 for 循环中）相比，递归定义的另一个方面是，它不是采用逐步方法（“做这个，然后做那个，然后做这个，最后就完成了”），而是更具声明性（“如果你得到这个输入，就做那个，否则就做这个”）。借助函数头中的模式匹配，这种特性更加明显。
如果您仍然没有理解递归的工作原理，也许阅读这里将会有所帮助。
说笑归说笑，递归结合模式匹配有时是编写简洁易懂的算法的最佳解决方案。通过将问题的每个部分细分为单独的函数，直到它们无法再简化，算法就变成了将来自短例程的正确答案组合起来（这与我们对快速排序的处理有点类似）。这种思维抽象在您日常的循环中也是可能的，但我认为在递归中更容易实现。您的里程可能会有所不同。
现在，女士们先生们，让我们来讨论一下：作者与他自己
- — 好吧，我认为我理解递归了。我理解它的声明性方面。我理解它具有数学根源，就像不变的变量一样。我理解您在某些情况下认为它更容易。还有什么吗？
- — 它遵循一种规律的模式。找到基本情况，写下来，然后所有其他情况都应该尝试收敛到这些基本情况以获得答案。这使得编写函数非常容易。
- — 是的，我知道了，您已经重复了很多次了。我的循环也能做到同样的事情。
- — 没错，我不会否认这一点！
- — 正确。我不理解的是，为什么您要费心编写所有这些非尾递归版本，如果它们不如尾递归版本好呢？
- — 哦，这仅仅是为了让事情更容易理解。从普通的递归（更漂亮，更容易理解）过渡到尾递归（理论上更有效率），这似乎是一个展示所有选项的好方法。
- — 好的，所以除了教育目的之外，它们毫无用处，我明白了。
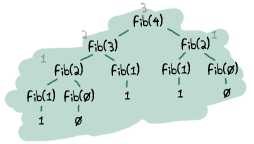
- — 不完全是。在实践中，您会发现尾递归和普通递归调用之间的性能差异很小。需要注意的方面是在应该无限循环的函数中，比如主循环。还有一种类型的函数始终会生成非常大的堆栈，速度很慢，并且如果未将其设为尾递归，可能会在早期崩溃。最好的例子是斐波那契函数，如果它不是迭代或尾递归，它将呈指数级增长。
您应该分析代码（我将在稍后介绍如何操作，我保证），找出导致代码变慢的原因，并进行修复。 - — 但是循环始终是迭代的，并且可以避免这个问题。
- — 是的，但是…但是…我美丽的 Erlang…
- — 难道不是这样好吗？所有这些学习，因为 Erlang 中没有 “while” 或 “for”。非常感谢，我要回到用 C 语言编程我的烤面包机了！
- — 别急！函数式编程语言还有其他优势！如果我们发现了一些基本模式，可以使我们在编写递归函数时更轻松，那么许多聪明人已经发现了更多模式，以至于您只需要自己编写很少的递归函数。如果您留下来，我会向您展示如何构建这样的抽象。但是，为此我们需要更强大的力量。让我来告诉你关于高阶函数…
